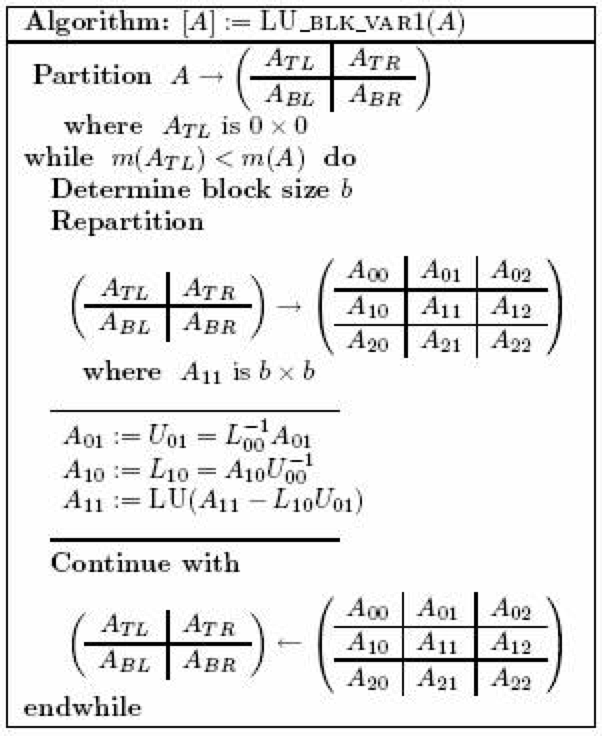
The key insight that enables the FLAME methodology is a new, more stylized notation for expressing loop-based linear algebra algorithms. This notation closely resembles how algorithms are naturally illustrated with pictures.

The FLAME project promotes the systematic derivation of loop-based algorithms hand-in-hand with the proof of their correctness. Key is the ability to identify the loop-invariant: the state to be maintained before and after each loop iteration, which then prescribes the loop-guard, the initialization before the loop, how to progress through the operand(s), and the updates. To derive the shown algorithm for LU factorization one fills in the below "worksheet". In the grey-shaded areas predicates appear that ensure the correctness of the algorithm.

A number of APIs have been defined for representing the algorithms in different languages. These include

FLaTeX	FLAME LaTeX commands for typesetting algorithms and worksheets
FLAME@lab	FLAME M-script (Matlab/Octave)
FLAMEC	FLAME API for the C programming language
FLASH	FLAMEC extension that allows matrices to be viewed as a hierarchy of submatrices
FLARE	The Formal Linear Algebra Recovery Environment (FLARE) adds algorithmic fault tolerance to some FLAME implementation
SuperMAtrix	Runtime system for scheduling task with submatrices using a Directed Acylic GraphG
Elemental	C++ library for distributed memory architectures